此是记录的按照前面做了以后

废话不多说，先调整周期性

1

trjconv_mpi -s md_0_1.tpr -f md_0_1.xtc -o md_0_1_noPBC.xtc -pbc mol -ur compact

全部选择

0(“System”)

老规矩，作图

1

gmx rms -s md_0_1.tpr -f md_0_1_noPBC.xtc -o rmsd.xvg -tu ns

全部选择碳链骨架

4(“Backbone”)

xmgrace作图以后，让人紧张的情绪膨胀

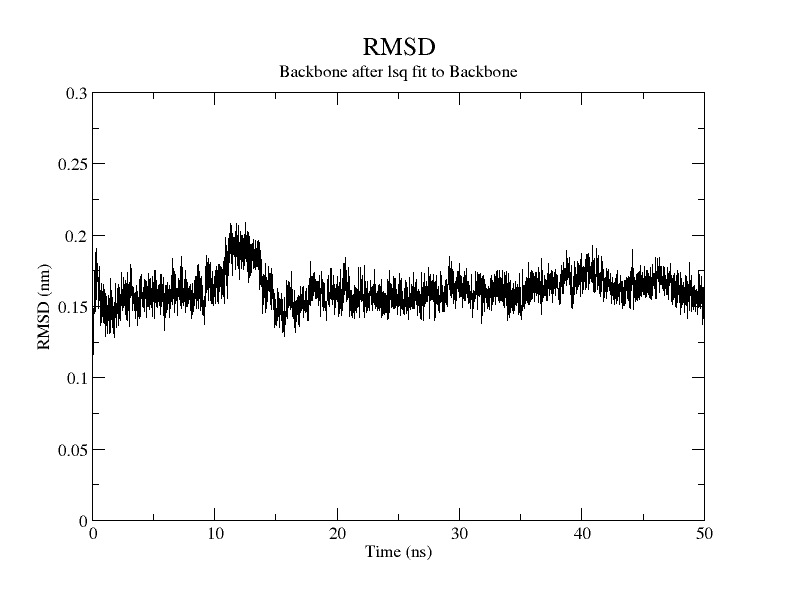
也不知道后面是不是真的是稳定了的说`````

在VMD中发现蒲中机-大连教我了另外一种方法能够使分子更加稳定PBC运动的方法，方法如下（注意代码每个人有差异）：

1.轨迹处理：

1
2
3
4
5
6
7

trjconv_mpi -f md_0_1.xtc -s md_0_1.tpr -pbc whole -ur compact -o mdwhole.xtc

trjconv_mpi -f mdwhole.xtc -s md_0_1.tpr -dump 0 -o 1stframe.pdb

trjconv_mpi -f mdwhole.xtc -s 1stframe.pdb -pbc nojump -o mdwholeNOjump.xtc

全部选择0 system

2.rmsd

1
2
3

gmx_mpi rms -s md_0_1.tpr -f mdwholeNOjump.xtc -o rmsd.xvg -tu ns

选择骨架4（Backbone）

3.rmsf

1
2
3

gmx_mpi rmsf -s md_0_1.tpr -f mdwholeNOjump.xtc -o rmsf.xvg -oq rmsf.pdb -res -b 15000

选择 3 ( C-alpha)

如图：

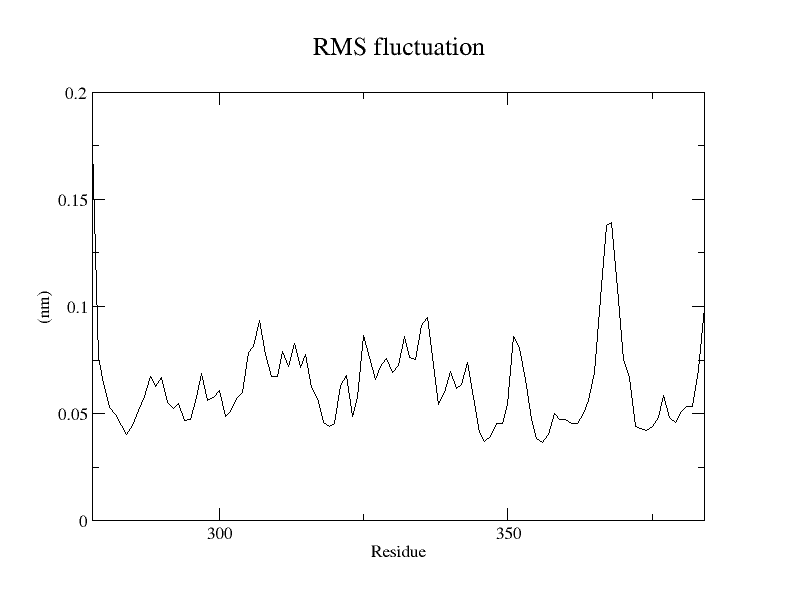
可以发现越是突变位点越发稳定

4.g_confrms比较结构差异

1
2
3

gmx g_confrms -f1 mAhR.pdb -f2 md_0_1.gro -o fit.pdb

#两次都选择骨架4（Backbone）

但是不知道为何生成的fit.pdb文件出来有一点问题，所以想尝试第二种方案

1
2
3

editconf_mpi -f md_0_1.gro -o md_0_1.pdb

editconf_mpi -f complex.gro -o mAhRaddh.pdb

在pymol中打开md_0_1.pdb，

1
2
3

输出select SOL,CL  ;delete sele

align structure2(md_0_1), structure1(mAhRaddh)

得到的结果图用cartoon作图结果如下：

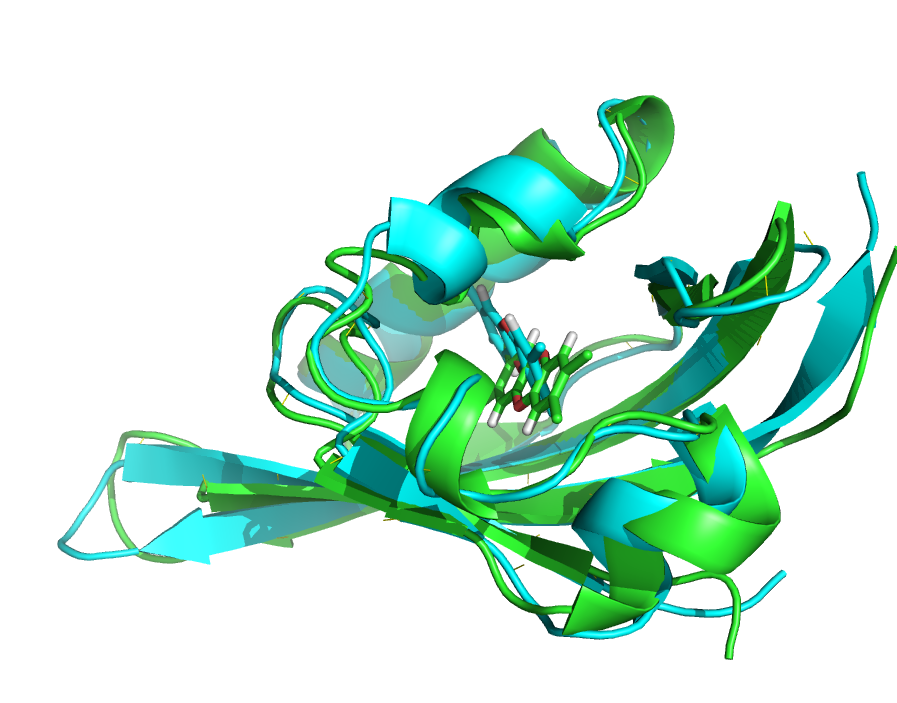
可以看出结构垭口和loop环的差别还是很大的，TCDD有一个翻转并且进一步深入口袋

5.豪猪图

采用Pymol画豪猪图，方法如前文

关键命令如下

1

modevectors pymolprotein1,pymolprotein2 ,cutoff=1.5,head_length=1.5,factor=2

结果如下：

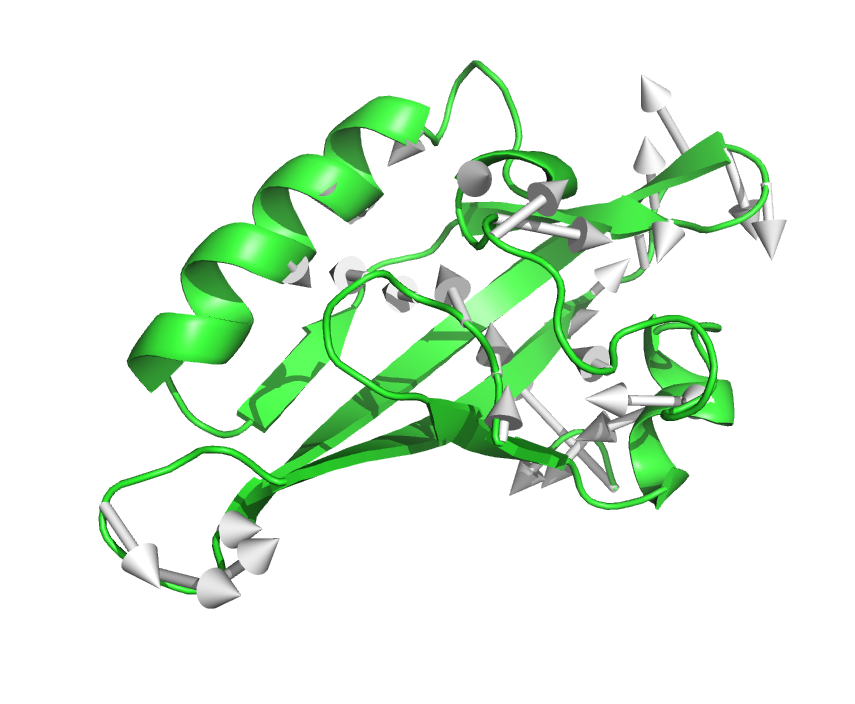
可以看出50ns AhR蛋白beta折叠和α螺旋并未进行剧烈的变动，仅仅为loop环结构使得接合口袋进一步的收缩，轻微的构象改变更好的说明同源建模过程中构象的准确性。

6.查看小分子的运动轨迹

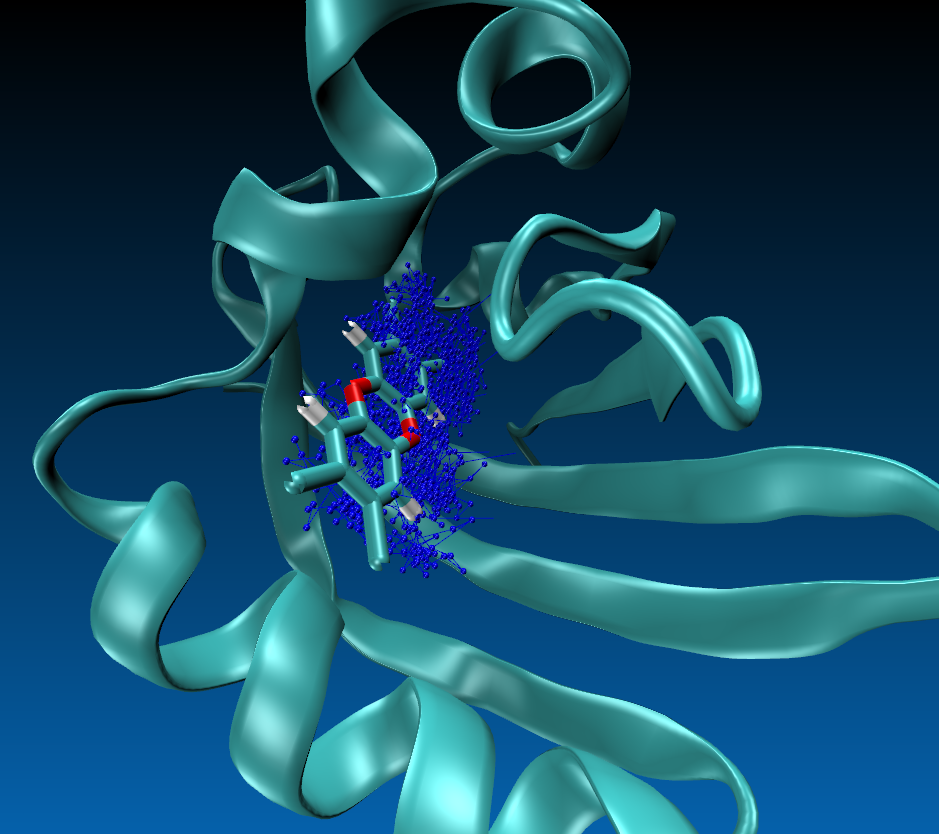
小圆点代表的为tcdd分子中每个原子1ns行走的位置，可以发现tcdd在接合口袋相当稳定，在一定波动范围波动，稍稍深入蛋白腔内部。

7.回旋半径的计算

蛋白质的回旋半径反应了蛋白质分子的体积和形状。同一体系的回旋半径越大，说明体系发生了膨胀。

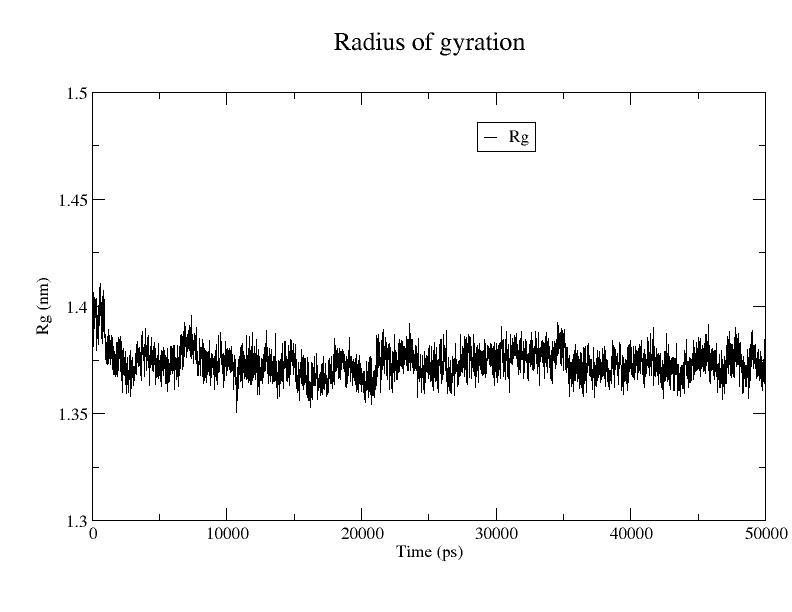
发现体系的回旋半径很稳定。

1
2
3

g_gyrate_mpi -f mdwholeNOjump.xtc -s md_0_1.tpr -o fws_gyrate.xvg

#选1 蛋白

8.dssp二级结构

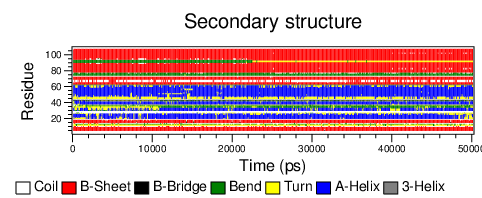
可以看出蛋白结构还是比较稳定，具体需要进一步研究

1
2
3
4

do_dssp -f md_0_1_noPBC.xtc -s npt.tpr -n index.ndx -o fwss.xpm -dt 100
xpm2ps -f fwss.xpm -o fwss.eps

convert fwss.eps fwss.bmp

9.计算最大螺旋性质

g_helix_mpi -s md_0_1.tpr -n index.ndx -f mdwholeNOjump.xtc -dt 100 gmx helix计算各种类型螺旋的性质. 程序首先会检查多肽段, 找到最长的螺旋部分, 这由氢键和φ/ψ角度确定的. 再将其拟合成一个绕z轴的理想螺旋, 以原点居中. 然后计算以下性质:

螺旋半径(radius.xvg输出文件). 这仅仅是二维平面内所有C~α~原子的RMS偏差, 计算方法sqrt((sum_i (x^2(i)+y^2(i)))/N), 其中N为骨干原子数. 理想螺旋的半径为0.23 nm. 扭转(twist.xvg输出文件). 计算每个残基的平均螺旋角. 对α螺旋此值为100度, 对3-10螺旋值会更小, 5-螺旋的值更大. 每个残基的上升量(rise.xvg输出文件). 每个残基的螺旋上升量以C~α~原子z坐标的差值表示. 对于理想螺旋此值为0.15 nm 总螺旋长度(len-ahx.xvg输出文件). 以nm为单位的总螺旋长度. 其值简单由平均上升量(见上文)乘上螺旋残基数(见下文)计算. 螺旋偶极. 只计算骨干原子的(dip-ahx.xvg输出文件). 与理想螺旋的RMS偏差, 仅根据C~α~原子计算(rms-ahx.xvg输出文件). 平均C~α~-C~α~二面角(phi-ahx.xvg输出文件) 平均φ和ψ角度(phipsi.xvg输出文件). 根据Hirst和Brooks方法计算的222 nm处的椭圆度

10.矩阵分析（PCA）

1

g_covar_mpi -s npt.gro -f mdwholeNOjump.xtc -o eigenvalues.xvg -xpma covapic.xpm

待编辑

参考文献：水中的溶菌酶教程

参考文献：漏斗网蜘蛛毒素肽的溶剂化研究: Amber99SB-ILDN力场

参考文献：dssp二级结构

参考文献：gromacs中的do_dssp的使用