g_mmpbsa之简单教程

MM/PBSA方法是一个非常有用的针对大分子特别是蛋白配体测亲和力很有用的方法。相对于自由能微扰(FEP)和热力学积分(TI),虽然准确度相对较低，但其计算量相对较小，比较适用于生物大分子体系。是一种对MD轨迹进行后处理以估计结合自由能的方法, 计算时会将溶剂视为均匀的连续介质, 并基于力场和隐式的连续介质模型, 对平衡轨迹中的许多帧进行平均, 以考虑温度的影响。其实该教程网上很多地方有，我之前也做过很多次，在这里仅做简单介绍，其实只是想引出后面的文章做一个系列。

安装教程

首先从这里下载对应版本,GROMACS2016和GROMACS2018版本都可以下载GROMACS-5.1. 版本。建议下载包括APBS版本，但改版本APBS无法进行多线程。记得把脚本也都下载下来。

预编译版本

1
2
3
4


tar -zxvf g_mmpbsa.tar.gz
cd bin
sudo cp g_mmpbsa /usr/local/bin/.
sudo cp energy2bfac /usr/local/bin/.

或导入$HOME中

1
2
3
4


tar -zxvf g_mmpbsa.tar.gz
cd bin
cp g_mmpbsa $HOME/bin/.
cp energy2bfac $HOME/bin/.

或设置环境变量

1

export PATH=${PATH}:/path/to/g_mmpbsa/bin

编译版本

略

下载教程包

你可以从此下载教程包，并进行解压:

1
2
3


tar -zxvf tutorial.tar.gz
cd tutorial
cd 1EBZ

其目录下包括HIV-1蛋白酶及其抑制剂的拓扑参数(tpr),索引文件(ndx)和轨迹(xtc)文件

GMXLIB环境变量

如果GROMACS为自定义安装，设置GMXLIB环境变量：

1

export GMXLIB=/opt/gromacs/share/gromacs/top

计算三个能量组件

结合能计算包括三个能量项目（a）真空中的势能，（b）极性溶剂化能和（c）非极性溶剂化能。这些能量可以一步计算或三步计算

三步计算

（a）真空中的势能

1

g_mmpbsa -f 1EBZ.xtc -s 1EBZ.tpr -n 1EBZ.ndx -pdie 2 -decomp

选择时第一次选择蛋白，第二次选择配体，计算将会得到energy_MM.xvg和contrib_MM.dat。energy_MM.xvg文件包含范德华力，静电相互作用以及蛋白质和抑制剂之间的非结合势能。 contrib_MM.dat包含每个残基对计算得到的非结合势能的贡献。

（b）计算极性溶剂化能

1

g_mmpbsa -f 1EBZ.xtc -s 1EBZ.tpr -n 1EBZ.ndx -i ../polar.mdp -nomme -pbsa -decomp

选择时第一次选择蛋白，第二次选择配体，计算将会得到polar.xvg和contrib_pol.dat。polar.xvg含有未结合蛋白，未结合抑制剂和蛋白抑制剂复合物的极性溶剂化能。contrib_pol.dat包含每个残基对计算的净极性溶剂化能的贡献。

（c）计算非极性溶剂化能非极性溶剂化能包含三种，分别为SASA，SAV和WCA-like模型，其实据我经验非极性溶剂化能只是很小的一部分能量，一般。这里按照教程来的介绍两个。

SASA模型

1

g_mmpbsa -f 1EBZ.xtc -s 1EBZ.tpr -n 1EBZ.ndx -i ../apolar_sasa.mdp -nomme -pbsa -decomp -apol sasa.xvg -apcon sasa_contrib.dat

SAV模型

1

g_mmpbsa -f 1EBZ.xtc -s 1EBZ.tpr -n 1EBZ.ndx -i ../apolar_sav.mdp -nomme -pbsa -decomp -apol sav.xvg -apcon sav_contrib.dat

一步计算

非常简单方便，也没有从教程中看出说差别

1

g_mmpbsa -f 1EBZ.xtc -s 1EBZ.tpr -n 1EBZ.ndx -i ../pbsa.mdp -pdie 2 -pbsa -decomp`

平均结合能计算

使用的脚本在此下载。注意需要python包含numpy和scipy。可以简单如下查看:

1

python

1
2


import numpy
import scipy

查看是否报错。若报错可以分别如下安装

1
2
3
4
5
6
7
8
9


# Ubuntu下，推荐
sudo apt-get install python-numpy
sudo apt-get install python-scipy

# pip
pip install numpy
pip install scipy

# conda，一般自带，推荐

最后命令如下

1

python MmPbSaStat.py -m energy_MM.xvg -p polar.xvg -a apolar.xvg (or sasa.xvg)

输出文件full_energy.dat和summary_energy.dat。summary_energy.dat文件内容如下:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22


#Complex Number:    1 
=============== 
   SUMMARY   
=============== 

 van der Waal energy      =        -334.587   +/-   15.514 kJ/mol 

 Electrostattic energy    =        -159.380   +/-   15.810 kJ/mol 

 Polar solvation energy   =         313.698   +/-   10.174 kJ/mol 

 SASA energy              =         -30.431   +/-    0.996 kJ/mol 

 SAV energy               =           0.000   +/-    0.000 kJ/mol 

 WCA energy               =           0.000   +/-    0.000 kJ/mol 

 Binding energy           =        -210.699   +/-   19.745 kJ/mol 

=============== 
    END     
=============== 

full_energy.dat包含Δ_E_MM, Δ_G_polar, Δ_G_nonpolar 和 Δ_G_binding随时间的关系。例如如下图:

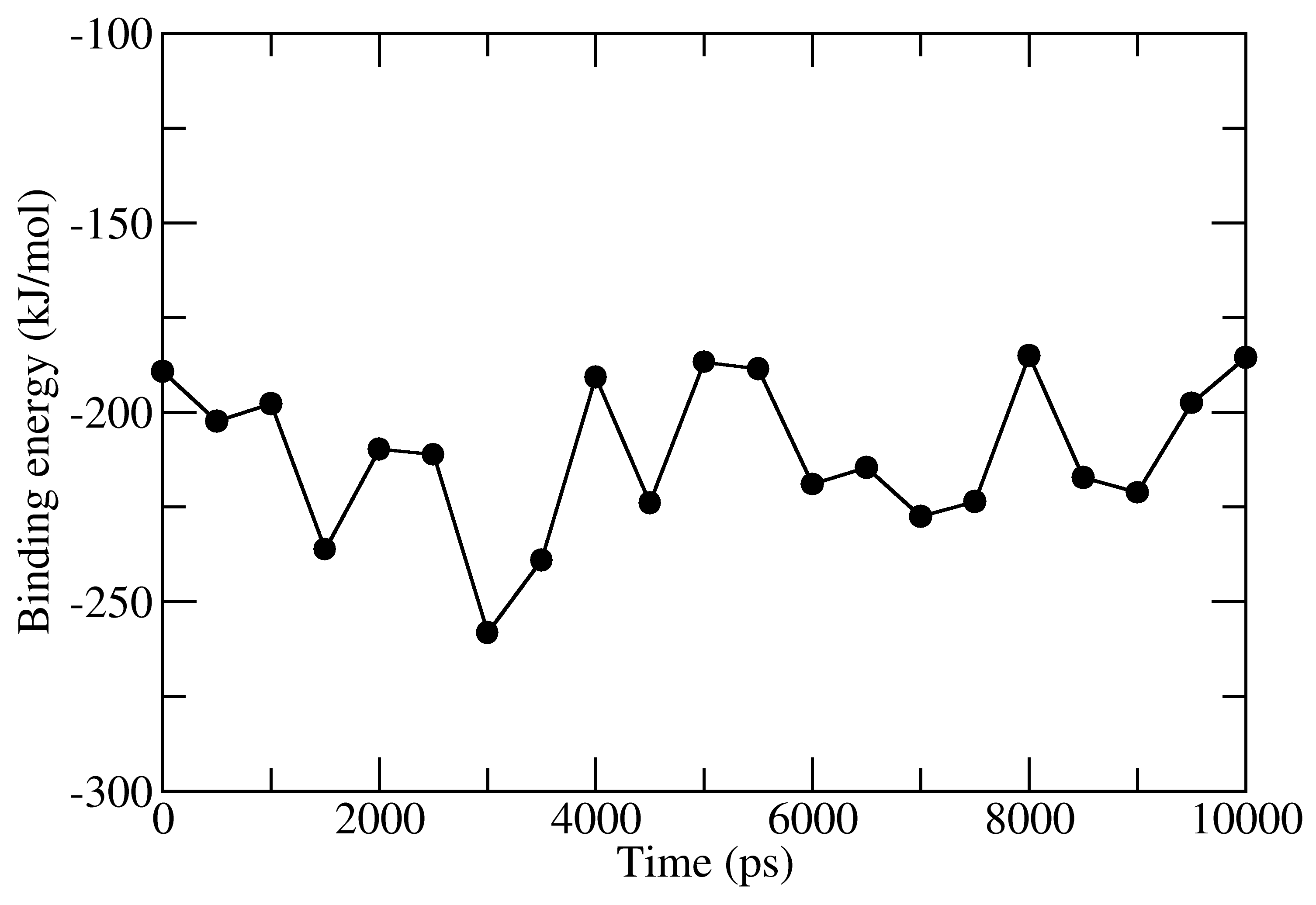
能量拆分

这个应该大家在很多地方都看过，就是看每个残基对小分子的贡献:

1

python MmPbSaDecomp.py -bs -nbs 2000 -m contrib_MM.dat -p contrib_pol.dat -a contrib_apol.dat

输出文件final_contrib_energy.dat和energyMapIn.dat.final_contrib_energy.dat包含对所有三个能量项（包括每个残基的结合能）的贡献能量以及标准误差的平均值。 energyMapIn.dat和xmgrace / matplotlib / gnuplot可用来绘制每个残基的贡献能量（需要删除抑制剂）。例如下图所示

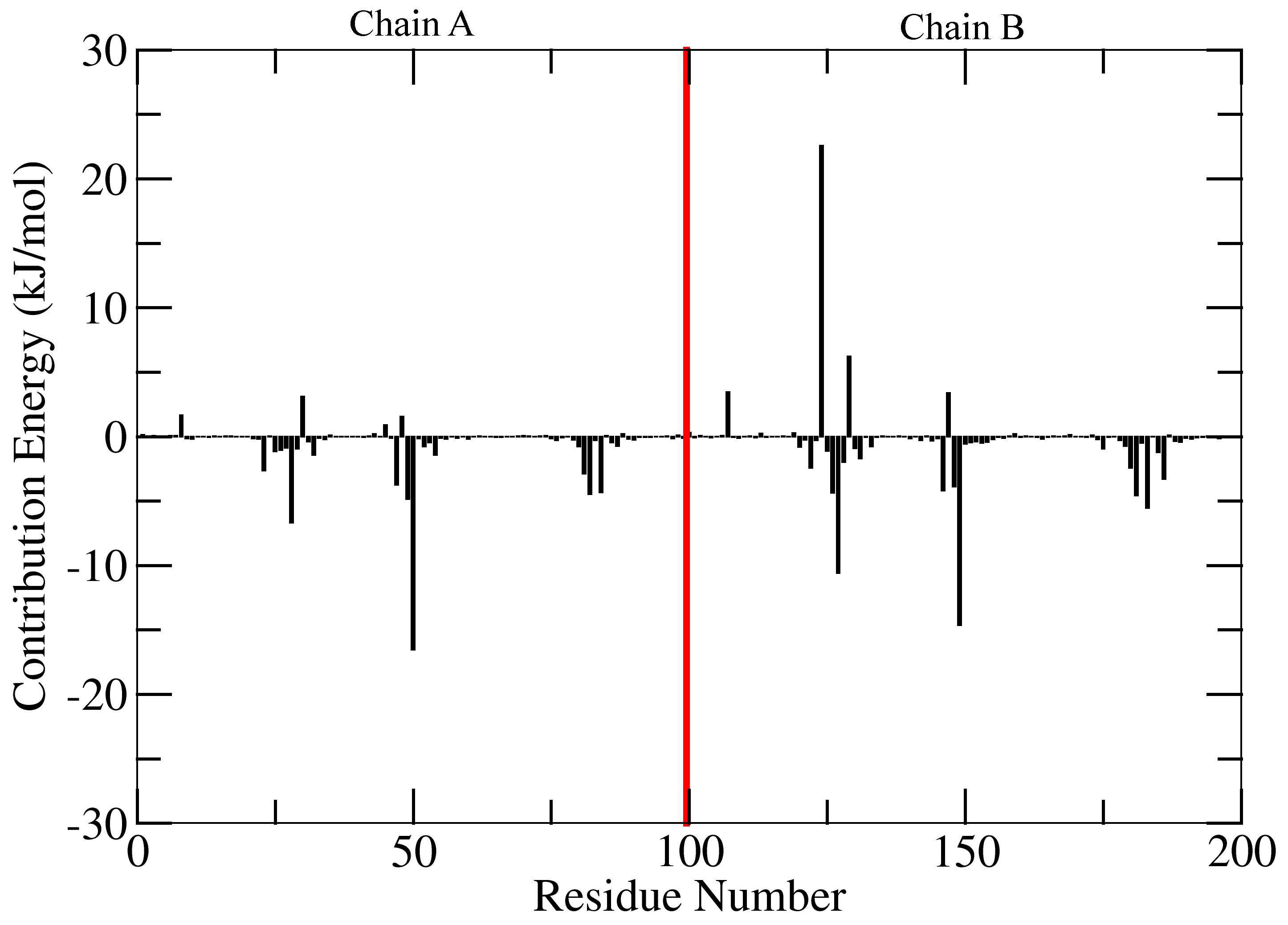
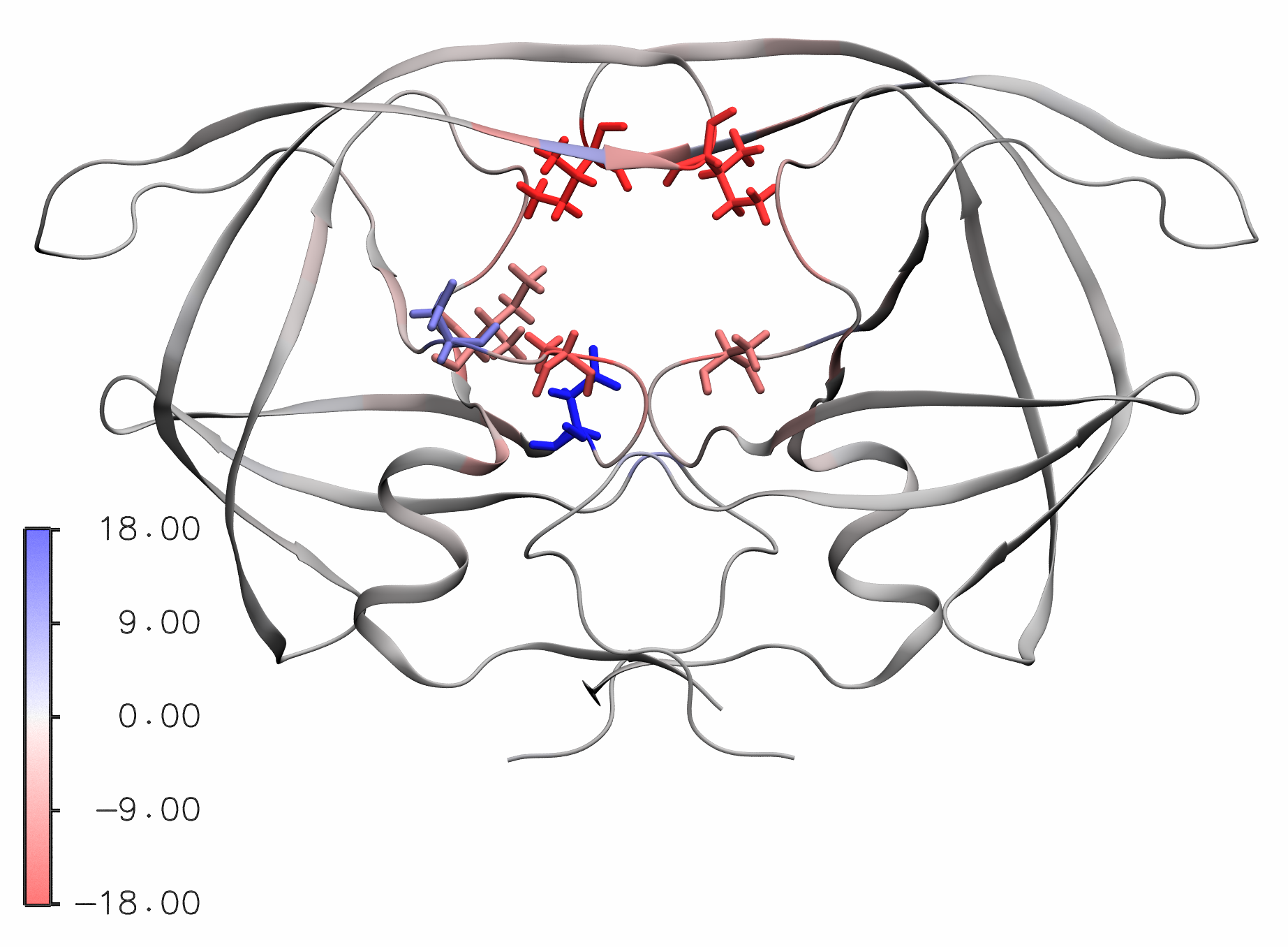
在VMD中可视化能量贡献

其主要是把其写入到PDB文件中B-factor 那一行，用B-factor 来进行做图。使用energy2bfac文件

1

energy2bfac -s 1EBZ_pbc_corrected.tpr -i energyMapIn.dat

输出文件complex.pdb, subunit_1.pdb 和 subunit_2.pdb,subunit_1.pdb 和 subunit_2.pdb分别表示第一选择组和第二选择组。在VMD中查看(其实pymol等工具也是可以滴):

1

vmd  subunit_1.pdb

在Drawing Method将图像展示改为NewCartoon . 将 Coloring Method 设为 Beta. 为了获得颜色尺度bar, Extension ⇒ Visulaization ⇒ Color Scale Bar. 选择 Autoscale: On. 选择 Label format: Decimal. 结果如下:

参考1:GROMACS教程:使用GROMACS计算MM-PBSA结合自由能参考2:g_mmpbsa