只是粗略翻译,未校正
此篇文章以RNA MD为舟,主要参考《RNA Structural Dynamics As Captured by Molecular Simulations: A Comprehensive Overview》一文3.2.3: Markov State Models一节。
近年来,马尔科夫状态模型(Markov State Model,MSM)方法在增强采样中得到了广泛的运用,成为热门的增强采样方法之一。马尔科夫模型的方法优势在于它能够从很多短的模拟中获取长时间的动力学特征,可以不需要事先定义反应坐标,从而避免了对整个动力学性质的简化或者是偏差。特别是最近几年大规模的平行计算资源的发展,更加促进了这一方法的应用。
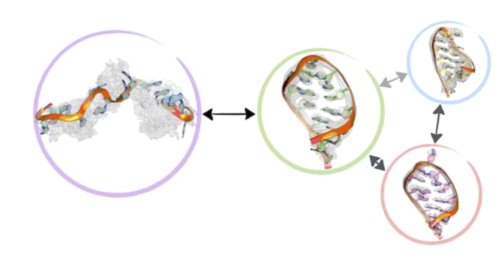
Fig 1. 马尔科夫状态模型, 广泛模拟分析,观察的状态被成簇聚类. 然后构建动力学矩阵,提供观察集群对之间转换的概率
在最近数十年,MSMs成为探索解释缓慢的生物分子复合物的运动并且其背后的理论日渐完善。MSM的工作流程简述如下:
-
MD数据聚集成一组有限的微观状态。每个微观状态均由许多结构组成,这些结构足够相似以至于在动力学项目中无法被区分。一个滞后时间,τ,被选为程序的时间离散化,并且在微观状态之间跃迁以对应滞后时间τ之间的步幅联系。
-
来自MD的信息(在滞后时间窗中观察的转变)被用来构建一个跃迁几率矩阵,T,其元素,Tij,表示了系统的几率始于微状态j,在时间τ之后将会跃迁到微状态i(请注意,T矩阵通常以其转置形式使用,然后将索引i和j的含义互换。)
-
系统在前面提到的微状态之间构建马尔科夫状态链,通过跃迁几率矩阵进行控制,因此时间t+τ时微观状态的概率分布仅取决于时间t时微观状态的分布,而不取决于系统的历史。换句话说,动力学模型之间是互不相关的进程,每个时间步骤τ,分子将会从一个微观状态“跳跃”到另外一个微观状态。
-
分析矩阵T的特征值谱以提取关于系统的热力学,动力学和动力学的信息。
离散的MSM结果旨在近似通过离散的程序估算模拟系统连续的动态。使用MSM,在一个离散的时间步长τ中可以进化单独的随机轨迹(微观状态的时间轨迹,例如:一个时间离散化的对应MD轨迹)或者微观状态的概率分布。MSM可以近似的极端被精确;换句话说,其可以提供和MD模拟相同的时间发展快照。比较其他的增强采样方法,其可以获得更加长时间尺度的结果(和热交换或者CV-基础的方法作为比较,后面会有时间进行记录)。MSM可以提供的信息有系统的动态参数和感兴趣的参数之间的跃迁比率,然而当系统的动态具有倾向性时,关于这些属性的信息通常会丢失。MSM的跃迁矩阵的特征值(eigenvalues)与特征向量(eigenvectors)的解释如下:第一个跃迁矩阵的特征向量是单位特征值并对应平稳分布向量,即该微状态的平衡概率;其它特征向量描述的为平衡的松弛过程,以及其对应的特征值, λ i,相关的时间尺度,ti,通过公式ti=-τ/ln(λi)进行降序排列。
MSM可以被广泛的用来帮助从一个长的MD轨迹中提取可阅读的信息,它反复和自发地对正在研究的罕见事件进行采样。如果模拟采样程序足够好,MSM可以被用来进行粗粒化模型的“创作”,为原始模拟数据提供非常需要的见解。或者,MSMs可以通过将所有轨迹跨越的集合进行离散化用来合并分隔的MD轨迹,并且计算在任何轨迹中的跃迁。这能够成为一个严格的结合信息,来自一个单质量模型的多个轨迹。
主要有两个手段来构建可信的MSM: i).将相空间的极其精细的离散化转化为微观状态 ii) 或者,以所谓的“中心(coring)”方法来计数对应于亚稳态的较大盆地之间的跃迁。 现在的研究一般使用第一种方法来解决。
构建MSM的第一步是将相空间离散化为微观状态。其可以通过使用不同的成簇方法和不同的标准进行完成。这一领域的一个重要进展是发展时滞独立成分分析( time-lagged independent component analysis,TICA).在这个方法中,输入变量的线性组合被构造以便找到具有最大自相关时间的自由度,并且因此预期在动力学分析中更重要。这使得后续的聚类可以在较低维度上完成,在主要TICA成分的空间中完成,通过模拟轨迹投影到最大的TICA成分上。TICA的方法和主成分分析(principal component analysis, PCA)方法较为相似(PCA方法也是MD轨迹分析的一个常用方法).PCA识别输入自由度与最高方差的线性组合,而TICA发现具有最高自相关时间的那些,即对应于模拟中发生的最慢过程。TICA可以从基于所有溶质原子的笛卡尔坐标的描述开始执行,或者使用在一些内部坐标上定义的描述,例如相关原子之间的二面角或配对距离.和其它降维方法相比,一个总需要当心的为一些重要的信息可能会被丢失,曲解快速时间尺度程序的描述。因为显著的结果被获取,TICA被推荐作为一个常规工具对于MD轨迹的坐标跃迁和降维.
将相空间离散化为有限个微态是MSM系统误差的主要来源.误差可以通过两个方式进行降低:增加滞时,τ,另一种方法为通过更加精细的离散化算法.在实践中,当处理非常精细长度的模拟,许多因素影响计算的质量。滞后时间本质上取决于系统的马尔可夫性和期望的时间分辨率.太短的滞时将会导致模型没有马尔可夫性。一般说来,与滞后时间相比,每个个体微观结构内的结构之间的相互转换必须是快速的.在蛋白和核酸体系中典型的τ值范围一般为0.1到10ns,通常通过观察隐含时间尺度的收敛来选择。具体描述如下:微观状态的数量应该足够大,以避免由于相位空间的粗糙化造成的分辨率损失,并且足够小对于有足够的数量以便于他们之间的跃迁(例如:拥有足够的统计学精度)并且矩阵大小是可控的。“中心”方法的运用是有差别的,其使用更加小的设置微态,其不需要覆盖系统完整的构象空间。
用现代方法模拟中等大小的生物分子,一个典型的使用MSMs方法至少需要102到104个微态。这种微观状态的数量使模型的可视化和直观分析变得不切实际。存在几种方法来克服这个问题,即利用MSM提供的动力学信息来构建系统的更粗略的表示,将MSM微观状态集合成少数亚稳态宏观状态.一个普遍使用的方法为Perron集群聚类分析(Perron-cluster cluster analysis,PCCA,更多信息可以通过这里还有这里进行了解)一种利用转换矩阵的特征向量的符号结构来定义MSM微观状态的最佳亚稳分区的方法.称为PCCA +和PCCA ++的更高级版本的方法为每个微观状态指定了成为给定亚稳态宏观成员的概率。
另一种减少模型的方法成为隐式马尔科夫模型(hidden Markov model, HMM).在这种方法中,系统被表示为隐藏的亚稳态宏观事件之间的马尔可夫链.这些宏观不是直接可观察的,而是通过观察微观态来测量的,微观态在每一步都是从一个分布概率中提取的,这个分布概率依赖于隐藏的宏观态来进行的.因此,假定可以使用附加(隐藏)变量来标记状态,并且其时间序列由观测变量的时间序列推断。HMM定义的态没有整齐的边界,并且一个给定的构象有可能同时参与多个宏观事件.
MSM方法一个关键的优势是能够监测,其不必假设全局平衡,而是假设MD在每个微观状态为局部平衡。实际上,对于模拟通过选择小的起始点,可以获得组装的相关短的轨迹,每个采样跃迁和不同的复合物步骤和缓慢设置改变相关。通过在MSM模型中结合这些轨迹,原则上,甚至可以重构甚至比任何单个轨迹的跨度更长的时间尺度上发生的过程。最大隐含时间尺度可以为用于构建MSM的所有MD轨迹的总持续时间的相同数量级.显然,初始点的选择必须十分慎重,必须确保没有重要的相变区域被忽略。
用于构建MSM的MD模拟有许多方法选择起始点.如果有,关于系统的先验知识可以用来初始化沿着有趣的构象变化的不同位置的模拟(例如,实验结构拥有多个构象可用),另一个方法是,新的模拟可以用来初始化成为一个“探索”模拟来获得新的感兴趣的构象。如果这个步骤在每次新的模拟中被递归地重复,它将产生MD级联的轨迹,对可用相空间的越来越大的区域进行采样.通过改变确定新轨迹的候选起始点的标准,可以沿着感兴趣的构象变化的路径驱动系统。这种方法通常被称为“自适应采样”,实际上它可以被视为增强采样技术的一个子类.另外一个强大的方法是初始结构从其它增强采样的方法中获得。
与所有旨在降低MD模拟计算成本的方法一样,MSM可能会以与其基本近似值和假设不一致的方式提供错误结果。因此,在从MSM得出任何结论之前,测试马尔可夫近似的有效性至关重要.这通常是通过观察隐含时间尺度ti的收敛来实现的,伴随着τ的值增大。隐含的时间尺度应该与马尔可夫系统中的τ无关,所以它们的收敛可以用来选择恰当的滞后时间(如果存在的话),这对应于真实动态的良好近似。指出以对数形式显示时间尺度的常见做法可能会由于对数函数的负凸性而给出收敛的错误印象。
重要的是要注意隐含时间尺度的收敛是马尔可夫性的一个必要但不充分的条件.当达到收敛时,最慢的隐含时间尺度应该对应于所研究系统中最慢的跃迁模式。它与以前的系统知识的比较可以提供一些关于全自由能景观是否被充分采样的提示。一个过短的隐含时间可能表示部分重要的自由能景观,在模拟数据集中完整的被缺失,MSM仅表征折叠景观的局部区域。当模拟太短或未初始化以充分覆盖相空间的相关部分时,可能会发生这种情况.例如研究折叠景观图,一系列的模拟初始点可能从一些解折叠中获得,获得的构象可能是强制解折叠或者高温模拟.对于通过漏斗机制快速折叠的分子,这可能效果很好。 然而,当折叠景观崎岖不平时,本质上遵从动态划分,景观的主要部分可能无法通过从“seeding”解折叠轨迹开始的模拟。
值得注意的是,研究必须始终对所研究的过程进行合理的整体评估,而不是仅仅依靠计算过程提供的数字。因为很多采样的中间过程都无法考虑周详.这限制了其的应用。MSM预测中另一个重要的不确定性来源是有限采样造成的统计误差。这个可以被验证通过马尔科夫链蒙特卡洛模拟(MCMC)的采样跃迁矩阵.将统计误差考虑在内是至关重要的,因为采样不良很容易导致与时间尺度本身相同数量级的相关隐含时间尺度上的不确定性.
例子:
r(A)3 的MSM分析
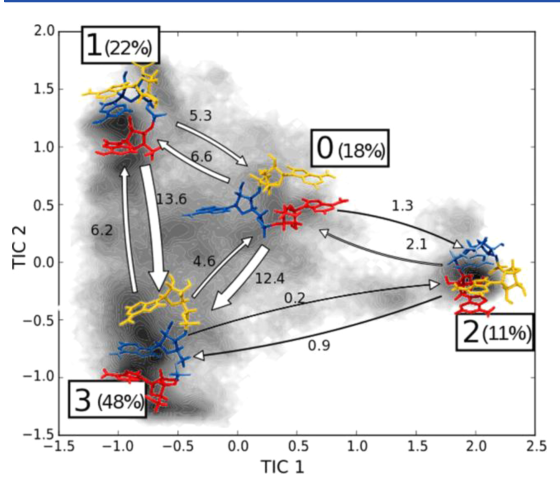
Fig 2. 腺嘌呤三核苷酸四个状态的隐式马尔科夫链模拟流程图,核苷酸根据序列位置进行着色(红,1;蓝,2;黄,3).百分比表示每个状态的平衡数;箭头粗细与跃迁态成比例,单位为μs-1.
MSM方法在近几年发展十分快速,过去许多受到欢迎的程序已经被更加好的方法所代替。这种方法成功的应用到许多蛋白体系的研究之中,现如今也进入到了RNA的世界。我们预计新的应用程序和工具将很快出现,并且将更严格地讨论方法适用性的限制。阴影表示投影在由两个主要TICA组件定义的平面上的模拟数据的分布。具体可以参考推荐阅读3.
推荐阅读: